






The earliest fully described Indian planetary models are two sets from the writer Aryabhata, both of which probably date from the early 6th century A.D. One model, called the sunrise system after its epoch date of sunrise on 18 February –3101, is conventionally attributed to a line of development called the Aryapaksa, and first appears in Aryabhata’s Aryabhatiya, although our complete understanding of the model is not established until the commentaries of Bhaskara, which date from about 628. The second, called the midnight system after its epoch date of midnight on 17/18 February –3101, is conventionally attributed to a line of development called the Ardharatrikapaksa, and first appears for us in Latadeva’s Suryasiddhanta included in Varahamahira’s Pancasiddhantika, which appeared in the second half of the 6th century, and then later in more detail in Brahmagupta’s commentary of 665. Both systems set their local meridian to Lanka, longitude about 76° east, latitude 0°.
From « The Equant in India: The Mathematical Basis of Ancient Indian Planetary Models”
Dennis Duke
Florida State University
http://people.scs.fsu.edu/~dduke/india8.pdf
The Sun

D = R x (e’/e)
With D = distance from
observer to Sun
Distance from M to equant = R x (e’ – e)
With R = radius of deferent
e’ = true eccentricity
e = mean eccentricity

Copyright © Robert Bywater & Jean-








We describe here the model Munjala developed around 930 CE
from earlier Indian models.
Our sources are the web page of Dennis Duke
http://people.scs.fsu.edu/~dduke/munjala2.pdf ,
the web page of Michael Nauenberg
http://physics.ucsc.edu/~michael/koll.html ,
the SAO / NASA Astrophysics Data System,
and the relevant article of Pingree.
The diagrams were established from the geocentric longitude of the Moon on 15 / 04 / 967 at 23:56 Angkor time (the choice of this date is explained in the chapter “Later diagrams”)


We have developed a theory about the relationship between the locations of the principal Khmer monuments (and in many instances their orientation and internal measurements) and components of enormous Indian planetary diagrams “drawn virtually” on the Angkorian ground using the parameters of the “Midnight System”.
The latter is one of the two geocentric planetary models which appeared in the texts of the Indian astronomer Aryabhata at the beginning of sixth century.
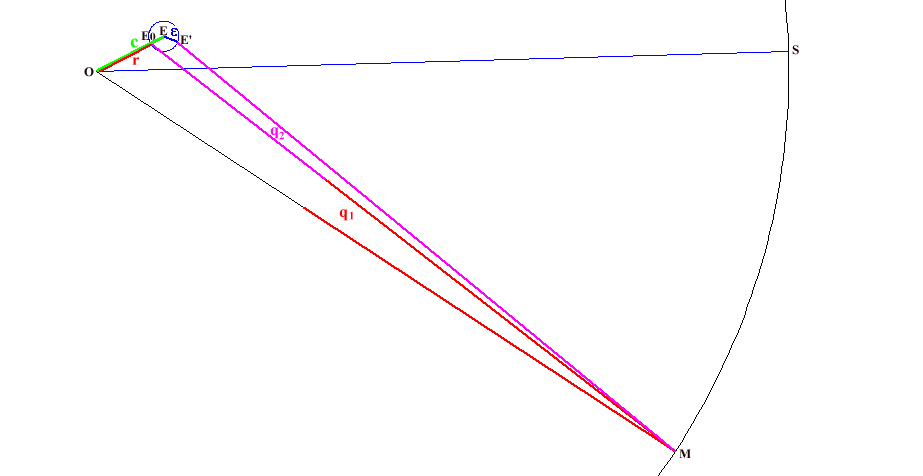
In the case of an outer planet (Saturn on the diagram), a circle called " deferent " is drawn from an " observer " which is supposed to stand on the Earth. The centre of another circle called the " Manda epicycle " rotates around the observer, travelling around the deferent.
The peripheral end of one radius (parallel to the apsides line) of this Manda epicycle determines the centre of another epicycle called the " Sighra epicycle ".
The location of an outer planet is on the circumference of the Sighra epicycle at the point where it is met by a radius drawn parallel to the direction of the Sun from the observer, (i.e. due east from the centre of the Sighra epicycle)
An important point, called the " equant ", is located on an apsides line drawn parallel to the radius of the Manda epicycle but running through the observer. The distance between the observer and the equant is twice the radius of the Manda epicycle. The mid-
The location of the Sighra epicycle’s centre is more clearly indicated on this magnified section of the Mercury diagram.
The equant of the inner planet is determined in the same way as that of an outer planet.
The role of the Manda epicycle is to take into account the variation of speed of the planet between the apogee and the perigee when it is travelling around its elliptical heliocentric orbit. The relative size of the Manda epicycle therefore is related to the eccentricity of its orbit.
The role of the Sighra epicycle is to take into account retrogrations of the planet. The relative size of the diameter of a Sighra epicycle (compared to the diameter of the deferent) is related to the proximity of the planet to the Earth and thus is relatively large for the planets Venus and Mercury.
The “concentric equant” model of Aryabhata
At the beginning of the sixth century, Aryabhata developed the “concentric equant” model : the Sun moves on a circle of radius R called a “deferent” whose centre is the earth (observer). That means the distance between the earth and the Sun is constant. The motion of the Sun is uniform as seen from a point called “equant” which is located at a distance R x e from the earth (observer) in the direction of the apogee (e = eccentricity). That means the motion of the Sun is not uniform as seen from the earth.
Details are provided by the following web page of Dennis Duke: http://www.dioi.org/equant.pdf
The oscillating epicycle model of Bhaskara
The Aryabhata model is mostly an algorithm which is not suitable in the context of sacred geography and we have discovered the Khmers drew the solar diagrams by using the epicycle equivalent of the Aryabhata model developed by Bhaskara during the seventh century. It is an epicycle model whose eccentricity is variable. A relevant animation of Dennis Duke can be seen on :
http://people.scs.fsu.edu/~dduke/pingree2.html
The solar diagrams we have discovered obey the rules of the Bhaskara model ie:
With:
e = mean eccentricity of the Bhaskara model
= eccentricity of the "concentric equant" model ( 0.0388889 in the table)
m = mean centrum (44.84° for 22 / 04 Sun)
“m” is the angle subtended at the observer, between the direction of the centre of the Bhaskara epicycle and the direction of the apsides line.
For an astronomer, “m” indicates the mean position (ecliptic longitude) of the Sun determined from the apsides line. It is the position of the centre of the Bhaskara epicycle.
The apsides line is the line from perigee to apogee. The ecliptic longitude of the latter is indicated in the table of the “Midnight” parameters.
e' = true eccentricity ( 0.040008 on 22 / 04)
It is the eccentricity of the solar diagrams “drawn” on the Angkorian ground.
Another notion, the equation of centre, plays a role in the solar diagrams we have discovered :
q = arcsin( e x sin(m) )
q = -
With q = equation of centre
In astronomy, the “equation” is an angle that is the difference between the true position and the mean position of a body. Thus:
q = t – m
q = 43.27° -
With t = true centrum
“t” is the angle subtended at the observer, between the direction of the Sun and the direction of the Apsides line.
For an astronomer, “t” indicates the true position (ecliptic longitude) of the Sun determined from the apsides line.
Note : the word “anomaly” maybe used for “centrum”.


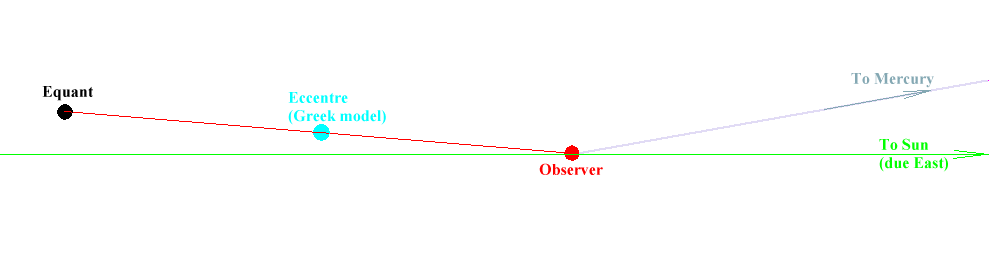
In the case of an inner planet (Mercury on the diagram), the centre of the Sighra epicycle is located on the straight line running through the observer and the Sun ie, in this case, on the geographical parallel of the observer.

The following diagrams show how the Indian and Khmer astronomers could determine the position of Saturn, Mercury and the Sun on 22 / 04 / CE 967 (Julian calendar) at midnight between 22nd and 23rd.
The " parallel of observer " is not a component of the " Midnight " system. It is a component of the diagrams drawn virtually on the ground. In Khmer sacred geography, indeed, the Sun is always supposed to lie due East of the observer (religious traditions).